da9dac

문제

접근 방식

k개의 초밥을 연속으로 먹었을 때 가장 다양한 종류의 초밥을 먹을 수 있는 경우를

구해야 하는 문제로 초밥을 k개 먹었을 때 중복 되지 않은 초밥이 몇 개인지를 찾으면 된다.

탐색은 이전의 투포인터 문제들과 마찬가지로 배열의 첫 인덱스를 기준으로

k개의 초밥을 먹을 때까지 탐색을 하고, 시작 인덱스를 1 증가시켜주면 된다.

// 연속으로 먹은 횟수
// 회전 벨트의 초밥 목록

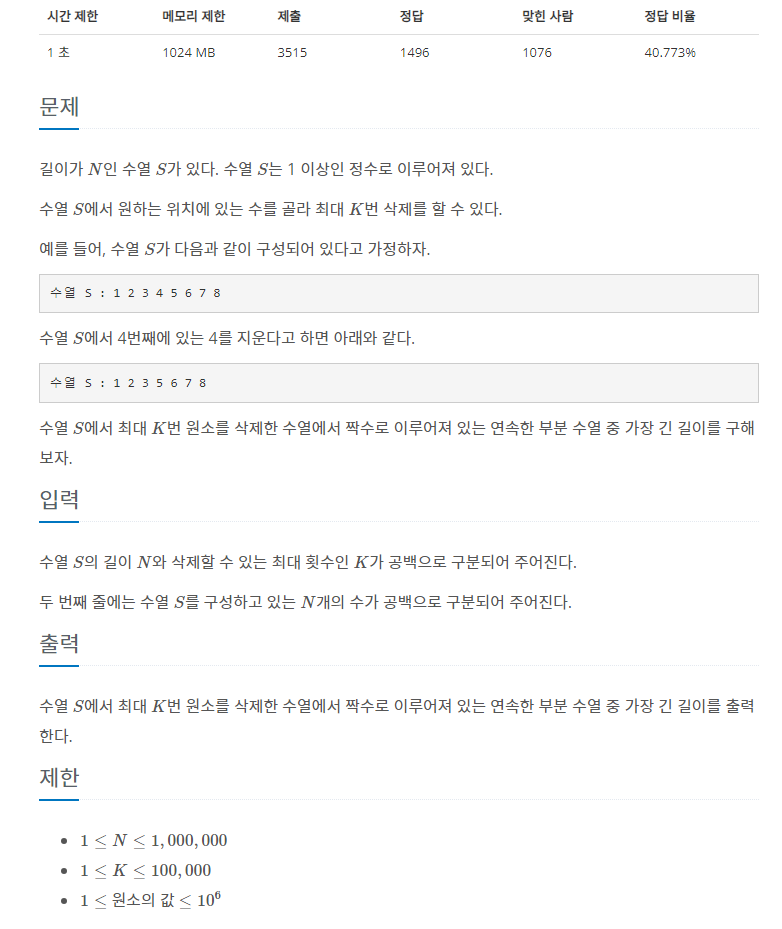
1	2	3	4k
7	9	7	30	2	7	9	25

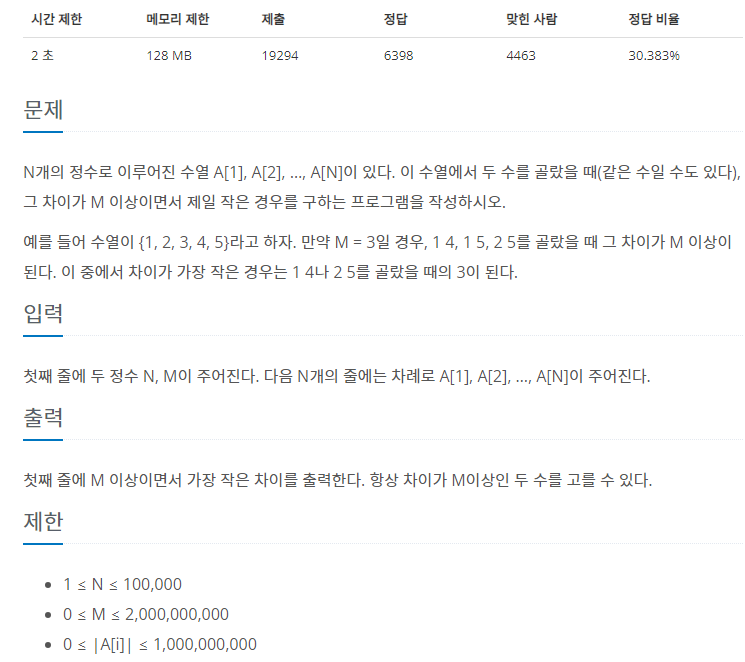
	1	2	3	4k
7	9	7	30	2	7	9	25

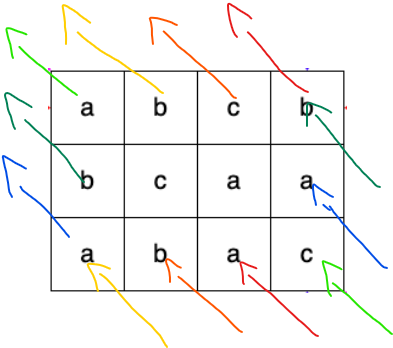
		1	2	3	4k
7	9	7	30	2	7	9	25

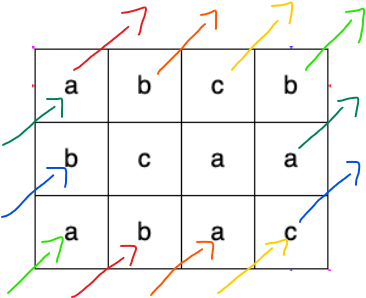
			1	2	3	4k
7	9	7	30	2	7	9	25

				1	2	3	4k
7	9	7	30	2	7	9	25

4k					1	2	3
7	9	7	30	2	7	9	25

3	4k				1	2
7	9	7	30	2	7	9	25

2	3	4k					1
7	9	7	30	2	7	9	25

탐색의 진행 과정은 위와 같다.

불리언 배열을 이용해 이미 등장한 초밥이라고 기록해두기엔

같은 초밥이 2번 이상 등장 했고, 시작 인덱스가 1 증가할 때마다

기존 시작 인덱스의 초밥을 안 먹었다고 false로 돌리면

해당 초밥을 더 먹었어도 안먹었다고 기록되는 문제가 생겨

정수 배열로 초밥의 등장 횟수를 기록했다.

그래서 탐색을 하면서 등장 횟수가 0인 경우에만

현재까지 먹은 종류를 1 증가시켜 주고,

쿠폰으로 얻는 초밥도 현재까지 먹지 않았을 경우에만 종류를 1 증가시켜 준다.

또한, 조심해야 할게 회전 초밥이기 때문에

배열의 인덱스를 벗어날 때는 다시 0번째 인덱스로 가게 해줘야 한다.

이러한 요소들만 생각하면서 코드를 짜주면 쉽게(여러 번 틀렸지만...) 풀 수 있다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		int n = Integer.parseInt(st.nextToken());
		int d = Integer.parseInt(st.nextToken());
		int k = Integer.parseInt(st.nextToken());
		int c = Integer.parseInt(st.nextToken());

		int[] belt = new int[n];
		int[] types = new int[d + 1];

		for (int i = 0; i < n; i++) {
			belt[i] = Integer.parseInt(br.readLine());
		}

		int end = 0;
		int continues = 0;
		int count = 0;
		int max = 0;

		for (int start = 0; start < n; start++) {
			while (continues < k) {
				if (types[belt[end]] == 0) count++;
				types[belt[end++]]++;
				if (end == n) end = 0;
				continues++;
			}

			if (types[c] == 0) {
				max = Math.max(count + 1, max);
			} else {
				max = Math.max(count, max);
			}

			types[belt[start]]--;
			if (types[belt[start]] == 0) count--;

			continues--;
		}

		System.out.println(max);
	}
}

문제

접근 방식

숫자를 k번만 삭제해서 짝수로만 이루어진 부분 수열 중

가장 긴 부분 수열의 길이를 구해야 한다.

첫 숫자부터 시작 포인트로 정하고 나머지 하나의 포인터를 사용해

다음 숫자들을 탐색해나가면 된다.

{1, 2, 3, 4, 5, 6, 7, 8}

예를 들어 위와 같은 수열이 주어졌고, 2번만 삭제할 수 있다면

짝수만 남겨야하니 홀수를 만날 때만 삭제해주고

다음에 홀수를 만났을 때 더이상 삭제할 기회가 남아있지 않다면

현재 까지 수열의 길이를 계산해주면 된다.

(현재 까지 수열의 길이 = 끝 포인터 - 시작 포인터 - 삭제한 홀수의 갯수)

// 남은 삭제 기회
// 숫자

1	1	0	0	x
1	2	3	4	5

2	1	1	0	0	x
2	3	4	5	6	7

1	1	0	0	x
3	4	5	6	7

2	1	1	0	0
4	5	6	7	8

순서를 살펴보면 위와 같다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		int n = Integer.parseInt(st.nextToken());
		int k = Integer.parseInt(st.nextToken());
		int[] arr = new int[n];

		st = new StringTokenizer(br.readLine());

		for (int i = 0; i < n; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}

		int end = 0;
		int max = 0;
		int rm = 0;

		for (int start = 0; start < n; start++) {
			while (end < n) {
				if (arr[end] % 2 != 0) {
					if (rm == k) break;
					rm++;
				}

				end++;
			}

			max = Math.max(max, end - start - rm);

			if (arr[start] % 2 != 0 && rm <= k) rm--;
		}

		System.out.println(max);
	}
}

문제

접근 방식

분명 이전 투포인터 문제들과 비슷한 문제라 쉽게 풀 수 있을거라 생각했는데

반환값의 범위를 잘못 생각해서 맞왜틀을 시전하느라 시간을 날려먹었다.

수열이 수의 범위가 1 ~ 100,000까지인 10만개의 수들로 이루어져 있어서

결과가 인트형으로 될줄 알았는데 혹시 싶어 long으로 바꿔보니 맞았다...

(왜 10만 * 10만을 10억으로 생각하고 있었지...새벽이라 정신줄을 놓고 했나보다)

{1, 2, 3, 2, 1, 1, 2, 3, 2, 1, 1, 2, 3, 2, 1}

위와 같은 수열이 주어졌을 때 중복되지 않는 수로만 이루어지는 경우를 살펴보자

{1, 2, 3, 2, 1, 1, 2, 3, 2, 1, 1, 2, 3, 2, 1}

// i[0]
1, 12, 123

// i[1]
2, 23

// i[2]
3, 32, 321

// i[3]
2, 21

// i[4]
1

// i[5]
1, 12, 123

// i[6]
2, 23

...

각 시작점을 기준으로 숫자들의 등장 여부를 기록해두면서

다음 숫자가 기존에 등장했던 숫자일 경우에는 중복된 숫자이기 때문에

이 시점을 브레이크 포인트로 잡고 현재 까지 연속된 부분 수열의 길이를

결과를 저장할 변수에 누적해서 더해주면 된다.

위에서도 언급했지만 이 때 결과를 저장할 변수를 long 타입으로 해야한다...

1 > 2 > 3 > 2(기존에 등장함)

즉, 1에서 출발 했을 때, 4번째 탐색한 숫자는 중복되기 때문에

저 시점에서 멈춘 후 현재 까지의 부분 수열인 {1, 2, 3}의 길이만큼

결과 변수에 합해준다.

2 > 3 > 2  (기존에 등장함)
3 > 2 > 1 > 1 (기존에 등장함)
2 > 1 > 1 (기존에 등장함)
1 > 1 (기존에 등장함)
1 > 2 > 3 > 2 (기존에 등장함)
2 > 3 > 2 (기존에 등장함)
...

이제 1로 시작하는 경우는 구했으니 시작 포인터를 1 증가 시킨 후에

위의 과정들을 반복하면 된다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		int n = Integer.parseInt(br.readLine());
		StringTokenizer st = new StringTokenizer(br.readLine());

		int[] arr = new int[n];

		for (int i = 0; i < n; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}

		boolean[] isUsed = new boolean[100001];
		long sum = 0;
		int end = 0;

		for (int start = 0; start < n; start++) {
			while (end < n) {
				if (isUsed[arr[end]]) break;
				isUsed[arr[end++]] = true;
			}

			sum += end - start;
			isUsed[arr[start]] = false;
		}

		System.out.println(sum);
	}
}

문제

접근 방식

주어진 수 n까지의 소수를 모두 구한 후에 투 포인터를 사용해

첫 번째 소수부터 기준으로 합이 n과 같거나 커질 때까지 수들을 합해주고

합이 n과 같은 경우에는 카운트를 1 증가시켜 주면서

현재 기준점이 끝날 때마다 합에서 현재 값을 빼준 후에

다음 기준점으로 넘어가면서 계산해 주면 된다.

a = {2 3 5 7 11 13 17 23 29 31 37 41}

n이 41일 때를 예로 들면, 2 ~ 41까지의 소수는 위와 같다.

sum		a[i]	count
2		2		1
5		3		2
10		5		3
17		7		4
28		11		5
41		13		6		v

39		-2		5
56		17		6		x
53		-3		5
48		-5		4
41		-7		3		v

30		-11		2
53		23		3		x
40		-13		2
69		29		3		x
52		-17		2		x
29		-23		1
60		31		2		x
31		-29		1
68		37		2		x
37		-31		1
78		41		2		x
41		-37		1		v

위의 과정을 살펴보면 2 ~ 13까지의 소수를 연속으로 더했을 때 41이 되니

카운트를 1 증가시켜 준 후에 다음 소수인 3부터 시작하기 위해 누적합에서 2를 뺀 후에

41 이상이 될 때까지 더하면 되고, 이 과정들을 반복해 주면  된다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		int n = Integer.parseInt(br.readLine());
		int size = 0;
		int count = 0;

		if (n == 1) {
			System.out.println(count);
			return;
		}

		boolean[] isPrime = new boolean[n + 1];
		int[] arr = new int[n + 1];
		int idx = 0;

		for (int i = 2; i <= n; i++) {
			if (!isPrime[i]) {
				size++;
				arr[idx++] = i;
				for (int j = i * 2; j <= n; j+=i) {
					isPrime[j] = true;
				}
			}
		}

		int end = 1;
		int sum = arr[0];

		for (int start = 0; start < size; start++) {
			while (sum < n && end < size) {
				sum += arr[end++];
			}

			if (sum == n) count++;

			sum -= arr[start];
		}

		System.out.println(count);
	}
}

문제

접근 방식

주어진 수들의 부분 수열의 합이 S 이상인 것 중에 가장 길이가 짧은

부분 수열을 찾아야 하는 문제로 이분 탐색이나 투 포인터를 사용해 풀 수 있는데

투 포인터를 연습 중이기 때문에 투 포인터를 사용해서 풀었다.

이전 글에서 풀었던 2230번 문제와 비슷한 문제라 풀기는 쉬웠는데

정렬을 해야 하는줄 알고 하고 풀다가 맞왜틀을 시전하느라 시간을 날렸다.

a = {5 1 3 5 10 7 4 9 2 8}  /  15

sum		a[i]	count
5		5		1
6		1		2
9		3		3
14		5		4
24		10		5		v
19		-5		4		v
18		-1		3		v
15		-3		2		o

위와 같이 10개의 수가 주어지고, 부분 수열의 합이 15이상인 경우를 살펴보면

시작 점을 0, 비교할 인덱스는 1부터 시작했을 때, 합이 15 이상이 될 때까지 더하다

15 미만이 될 때까지 넣은 순서대로 값을 다시 빼주고

다시 15 이상이 될 때까지 더해주는 것을 반복하면서

가장 짧은 수열의 길이를 찾아주면 된다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		int n = Integer.parseInt(st.nextToken());
		int s = Integer.parseInt(st.nextToken());

		st = new StringTokenizer(br.readLine());
		int[] arr = new int[n];

		int x = 0;

		for (int i = 0; i < n; i++) {
			int num = Integer.parseInt(st.nextToken());
			arr[i] = num;
			x += num;
		}

		if (x < s) {
			System.out.println(0);
			return;
		}

		int end = 1;
		int count = 1;
		int sum = arr[0];
		int min = Integer.MAX_VALUE;


		for (int start = 0; start < n; start++) {
			while (sum < s && end > start && end < n){
				count++;
				sum += arr[end++];
			}

			if (sum >= s) {
				min = Math.min(min, count);
			}

			count--;
			sum -= arr[start];
		}

		System.out.println(min);
	}
}

문제

접근 방식

두 수의 차이가 m 이상이면서 가장 작은 경우를 구해야 하는데

간단하게 이중 반복문으로도 풀 수는 있지만 입력의 크기를 생각하면

시간초과 때문에 다른 방법을 사용해야 한다.

골드 문제지만 투 포인터를 사용해서 풀면 간단하게 풀 수 있는 문제로

6개의 수가 주어졌을 때 차이가 3 이상인 수 중에서 가장 작은 경우를 찾아보겠다.

1 3 5 7 8 10

우선 위와 같이 주어진 수들이 정렬되어 있을 때

순서대로 비교할 기준을 처음인 1과 나머지 숫자들을 차이가 3 이상이 될 때까지 비교해보면

1 - 3 >> 2
1 - 5 >> 4

1 - 7 >> 6
1 - 8 >> 7
1 - 10 >> 9

5와 비교 했을 때 차이가 4로 처음으로 3보다 커지는데

이후의 비교는 차이가 점점 커지기 때문에 의미가 없다는 것을 알 수 있다.

그래서 차이가 처음으로 3보다 커진 경우에는 비교하는 기준 인덱스를

1에서 3으로 바꿔 준 후에 다시 비교를 해주면 된다.

3 - 5 >> 2
3 - 7 >> 4

3을 기준으로 비교하다 보면 마찬가지로 7과의 차이가 4일 때

기준이 다시 바뀌게 되고

5 - 7 >> 2
5 - 8 >> 3

5를 기준으로 다시 비교해보면 8과의 차이가 3으로

이후의 수들을 굳이 비교안해도 정답이 확실하기 때문에

탐색을 종료할 수 있다.

골드 문제지만 이렇게 투 포인터의 개념만 안다면 쉽게 풀 수 있다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		StringTokenizer st = new StringTokenizer(br.readLine());

		int n = Integer.parseInt(st.nextToken());
		int m = Integer.parseInt(st.nextToken());

		int[] arr = new int[n];

		for (int i = 0; i < n; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}

		Arrays.sort(arr);

		int s = 0;
		int e = 1;
		int min = Integer.MAX_VALUE;

		while (e < n) {
			int minus = arr[e] - arr[s];
			if (minus == m) {
				min = m;
				break;
			}

			if (minus >= min) {
				s++;
				continue;
			}

			if (minus > m) {
				min = minus;
				s++;
			}
			else e++;
		}

		System.out.println(min);
	}
}

문제

접근 방식

문제에 나오는 환형의 개념 중에서 대각선 이동이 살짝 햇갈렸던 문제인데

위의 사진들처럼 대각선 이동 중 인덱스를 벗어나는 상황을 살펴보면

인덱스가 음수가 되는 경우에는 가장 아래줄의 왼쪽이나 오른쪽으로 한칸 이동

양수가 되는 경우에는 가장 첫줄의 왼쪽이나 오른쪽으로 한칸 이동해주면 된다.

나머지 상하좌우 이동도 환형을 생각해주면서 백트래킹으로 단어를 조합만 해주고

이를 맵을 사용해서 각 단어별로 카운팅을 해줬다.

설명은 이해가 잘 안갔는데 막상 풀어보니 난이도 자체는 어렵지 않았던 문제다.

풀이

public class Main {

	private static int n;
	private static int m;
	private static int min = Integer.MAX_VALUE;
	private static int max = 0;

	private static int[] dx = {-1, 1, 0, 0, -1, -1, 1, 1};
	private static int[] dy = {0, 0, -1, 1, -1, 1, -1, 1};
	private static char[][] world;
	private static char[] chars;
	private static boolean[][] isUsed;

	private static Map<String, Integer> wordCount = new HashMap<>();

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		StringBuilder sb = new StringBuilder();

		n = Integer.parseInt(st.nextToken());
		m = Integer.parseInt(st.nextToken());
		int k = Integer.parseInt(st.nextToken());

		world = new char[n][m];
		isUsed = new boolean[n][m];

		for (int i = 0; i < n; i++) {
			world[i] = br.readLine().toCharArray();
		}

		String[] favorites = new String[k];

		for (int i = 0; i < k; i++) {
			String word = br.readLine();
			favorites[i] = word;
			max = Math.max(word.length(), max);
			min = Math.min(word.length(), min);
		}

		chars = new char[max];

		for (int i = 0; i < world.length; i++) {
			for (int j = 0; j < world[i].length; j++) {
				if (isUsed[i][j]) continue;
				isUsed[i][j] = true;
				chars[0] = world[i][j];
				makeWord(1, i, j);
				isUsed[i][j] = false;
			}
		}

		for (String favorite : favorites) {
			Integer count = wordCount.get(favorite);
			sb.append(count != null ? count : 0).append("\n");
		}

		System.out.println(sb);
	}

	private static void makeWord(int size, int x, int y) {
		if (size >= min) {
			String word = new String(Arrays.copyOfRange(chars, 0, size));
			wordCount.put(word, wordCount.getOrDefault(word, 0) + 1);
		}

		if (size == max) return;

		for (int dir = 0; dir < 8; dir++) {
			int nx = dx[dir] + x;
			int ny = dy[dir] + y;

			if (nx < 0) nx = n - 1;
			if (nx >= n) nx = 0;
			if (ny < 0) ny = m - 1;
			if (ny >= m) ny = 0;

			isUsed[nx][ny] = true;
			chars[size] = world[nx][ny];
			makeWord(size + 1, nx, ny);
			isUsed[nx][ny] = false;
		}
	}
}

문제

접근 방식

처음 풀어보는 DP문제로 백트래킹으로도 풀 수 있지만 시간제한이 빡빡한 문제이기 때문에

DP로 효율적으로 풀어야 풀 수 있는 문제다.

2를 1로 만드는 경우
2 - 1 >> 1
2 / 2 >> 1

3을 1로 만드는 경우
3 / 3 >> 1
3 - 1 - 1 >> 2

4를 1로 만드는 경우
4 / 2 / 2 >> 2
4 / 2 - 1 >> 2
4 - 1 - 1 / 2 >> 3
4 - 1 - 1 - 1 >> 3

가장 작은 경우를 예로 들어 2 ~ 4가 1이 되는 경우를 살펴보면 위와 같은데

4 / 2 / 2 순서로 계산하여 1이 되는 경우에는 숫자의 변화는 4 > 2 > 1이 될 것이고

해당 숫자의 인덱스에 계산 횟수를 기록한다 치면 {0, 2, 1, 0, 0} 이 된다.

여기서 알 수 있는 점은 연산을 할 때마다 연산 결과의 인덱스가 이전 횟수 + 1이라는 것이다.

count[n] = 0

count[n - 1] = count[n] + 1
count[n / 2] = count[n] + 1
count[n / 3] = count[n] + 1

즉, 위와 같이 인덱스가 점점 줄어들면서 1에 다다르게 됫을 때 최종 값이

가장 적은 연산 횟수인 것을 알 수 있다.

이를 그대로 코드로 구현하면 되는데 우선 DP 테이블에 연산 결과에 해당하는 인덱스까지

몇 번의 연산을 사용했는지를 기록하게 하고, 1부터 n까지 반복문을 돌면서

k - 1, k / 2, k / 3 번째 인덱스들에 이전까지의 연산 횟수 + 1에 해당하는 값들을 저장해준다.

주의해야 할 점은 2와 3으로 나누는 경우는 완전히 나누어 떨어질 때만 가능하며

나누는 경우가 1을 빼는것보다 효율적인지를 판단하기 위해

둘 중 더 작은 값을 기준으로 저장해줘야 한다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		int n = Integer.parseInt(br.readLine());
		int[] counts = new int[n + 1];

		for (int i = 2; i <= n; i++) {
			counts[i] = counts[i - 1] + 1;
			if (i % 2 == 0) counts[i] = Math.min(counts[i], counts[i/2] + 1);
			if (i % 3 == 0) counts[i] = Math.min(counts[i], counts[i/3] + 1);
		}

		System.out.println(counts[n]);
	}
}