문제
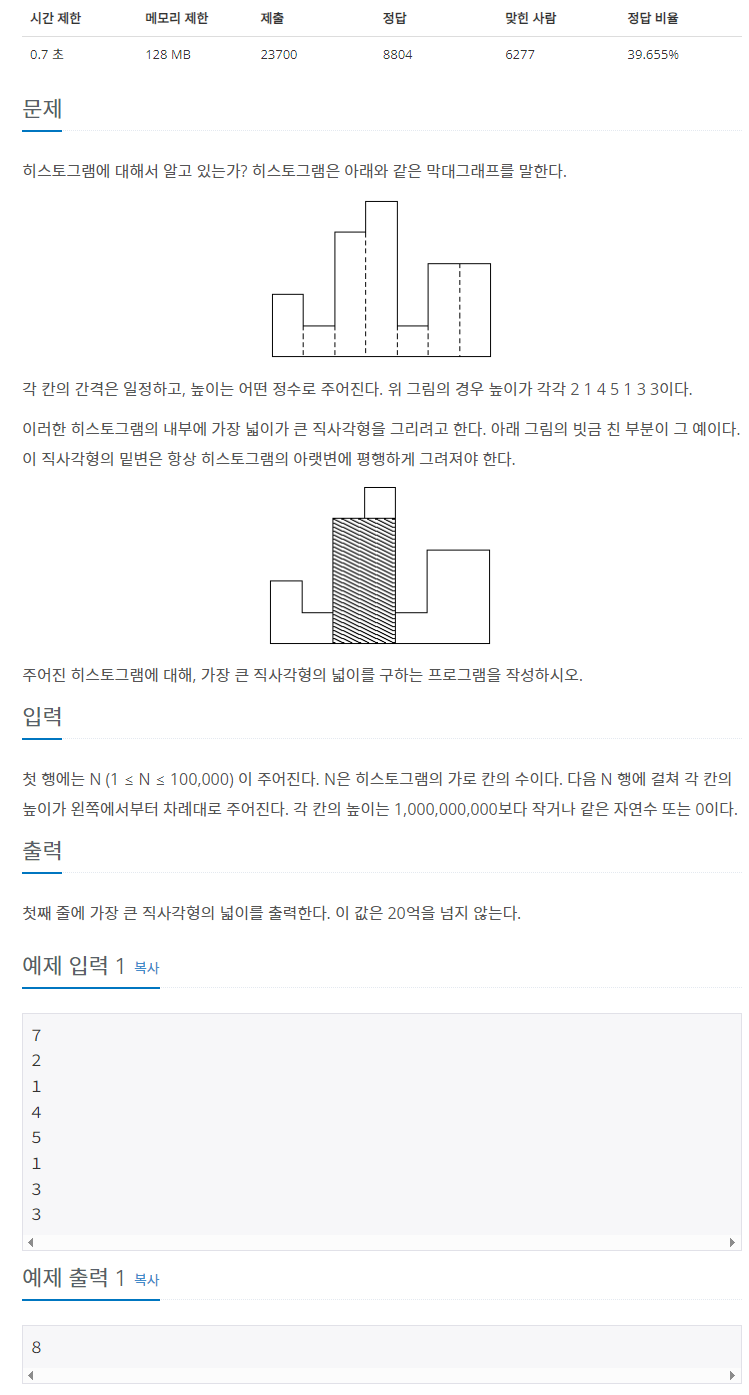
접근 방식
세그먼트 트리를 사용해서 풀 수 있는 문제라는데 아직 배우지 않아서
세그먼트 트리에 대해서 간단하게 검색해 보니 재귀를 사용한 방식이라
스택으로도 풀 수 있는 문제라서 스택을 사용해서 풀어봤다.
눈으로는 이해가 쉽고 넓이가 바뀌는 구간을 찾아서 계산을 해주면
해결된다는 사실도 머리로는 쉽게 이해가 가능하지만
구현하려니 막상 머리가 안 돌아갔다...
우선, 간단하게만 생각해 보면
직사각형의 넓이는 다음 막대그래프의 높이가 낮아질수록
최대로 가능한 넓이가 작아질 것이고
다음 막대그래프의 높이가 같거나 높아야
최대로 가능한 넓이가 유지되거나 커진다.
정리하면 각각의 높이가 4 5 5인 막대그래프가 연속해서 존재하면
가능한 최대 높이는 가장 낮은 높이인 4와 연속된 그래프의 개수 3을 곱한
12가 나온다는 것을 알 수 있고
각각의 높이가 4 3 2인 그래프가 연속해서 존재하면
가능한 최대 높이는 가장 낮은 높이인 2와 연속된 그래프의 개수 3을 곱한
6이 나온다는 말이다.
즉, 스택에 구간이 바뀔 때까지 계속해서 쌓아주다가
구간이 바뀔 때 쌓아둔 그래프들은 비슷한 높이가 연속적으로 존재하기 때문에
모두 계산해 주면 그 구간의 최댓값을 구할 수 있다.
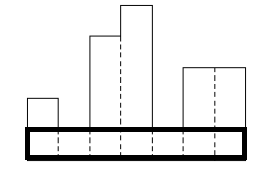
조심해야 할 부분은 위와 같이 이전까지의 모든 값들을 다 계산해줘야 한다는 것인데
지금의 경우에는 아래 표시한 영역의 넓이는 7이라 정답이 아니지만
만약 아래 표시한 영역의 넓이가 가장 큰 경우에 이 부분을 체크하지 않으면
잘못된 정답을 얻게 된다.
그래서 스택에서 값을 하나씩 꺼낼 때마다 각각 계산을 하여
현재까지 기록된 최댓값이랑 비교해서 저장해줘야 한다.
풀이
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n + 2];
for (int i = 1; i <= n; i++) arr[i] = Integer.parseInt(br.readLine());
Stack<Integer> histograms = new Stack<>();
histograms.push(0);
int max = 0;
for (int i = 1; i <= n + 1; i++) {
while (!histograms.isEmpty()) {
int prev = arr[histograms.peek()];
if (prev <= arr[i]) break;
histograms.pop();
max = Math.max(max, prev * (i - histograms.peek() - 1));
}
histograms.push(i);
}
System.out.println(max);
}
}
'Java > Algorithms' 카테고리의 다른 글
| [백준] 1463번 : 1로 만들기 (0) | 2023.12.11 |
|---|---|
| [백준] 15683번 : 감시 (0) | 2023.11.18 |
| [백준] 7795번 : 먹을 것인가 먹힐 것인가 (1) | 2023.11.16 |
| [백준] 2910번 : 빈도 정렬 (1) | 2023.11.16 |
| [백준] 1181번 : 단어 정렬 (0) | 2023.11.16 |