728x90
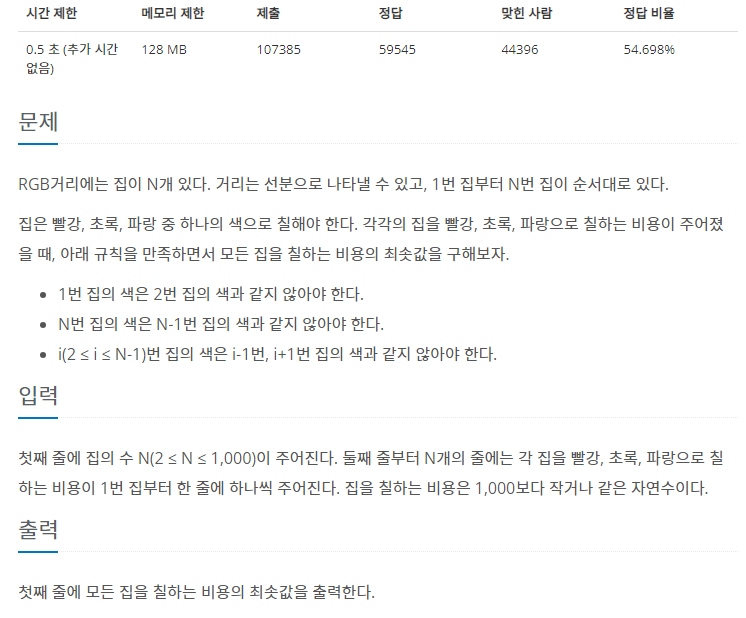
문제
접근 방식
백트래킹이나 다중반복문으로도 풀 수 있는 문제지만
시간제한을 보면 그렇게는 풀 수 없는 문제들이라 DP를 사용해서 풀었다.
1 ~ N번 집까지 있을 때, N번 집을 가장 적은 비용으로 칠할 수 있는 경우는
N-1번째 집을 칠한 경우 중 가장 적은 비용 + 현재 칠할 수 있는 색깔이다.
R G B
26 40 83
49 60 57
13 89 99
위와 같이 3개의 집과 각 집을 칠하는 색깔별 비용이 주어졌을 때를 살펴보면
26 -> 60 OR 57 -> 13 OR 99 / 13 OR 89
40 -> 49 OR 57 -> 89 OR 99 / 13 OR 89
83 -> 49 OR 60 -> 89 OR 99 / 13 OR 99
이전 집을 칠한 색깔을 제외한 각각의 색깔들 별로 칠할 수 있다.
DP 테이블을 각 집별로 3가지 색깔을 기록할 수 있게 만든 후에
이전 집의 최소 비용인 경우 + 현재 색깔을 칠하는 비용을 합해주면서
테이블을 모두 채워준 후에 마지막 집을 칠한 3가지 경우 중
가장 비용이 적은 경우를 출력해 주면 된다.
풀이
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int n = Integer.parseInt(br.readLine());
int[][] rgb = new int[n][3];
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < 3; j++) {
rgb[i][j] = Integer.parseInt(st.nextToken());
}
}
int[][] dp = new int[n][3];
dp[0][0] = rgb[0][0];
dp[0][1] = rgb[0][1];
dp[0][2] = rgb[0][2];
for (int i = 1; i < n; i++) {
int r = rgb[i][0];
int g = rgb[i][1];
int b = rgb[i][2];
int pr = dp[i - 1][0];
int pg = dp[i - 1][1];
int pb = dp[i - 1][2];
dp[i][0] = Math.min(pg, pb) + r;
dp[i][1] = Math.min(pr, pb) + g;
dp[i][2] = Math.min(pr, pg) + b;
}
System.out.println(Math.min(dp[n - 1][0], Math.min(dp[n - 1][1], dp[n - 1][2])));
}
}
'Java > Algorithms' 카테고리의 다른 글
| [백준] 11727번 : 2×n 타일링 2 (1) | 2023.12.18 |
|---|---|
| [백준] 11726번 : 2×n 타일링 (1) | 2023.12.18 |
| [백준] 20922번 : 겹치는 건 싫어 (1) | 2023.12.17 |
| [백준] 2531번 : 회전 초밥 (1) | 2023.12.17 |
| [백준] 22862번 : 가장 긴 짝수 연속한 부분 수열 (large) (0) | 2023.12.16 |