da9dac

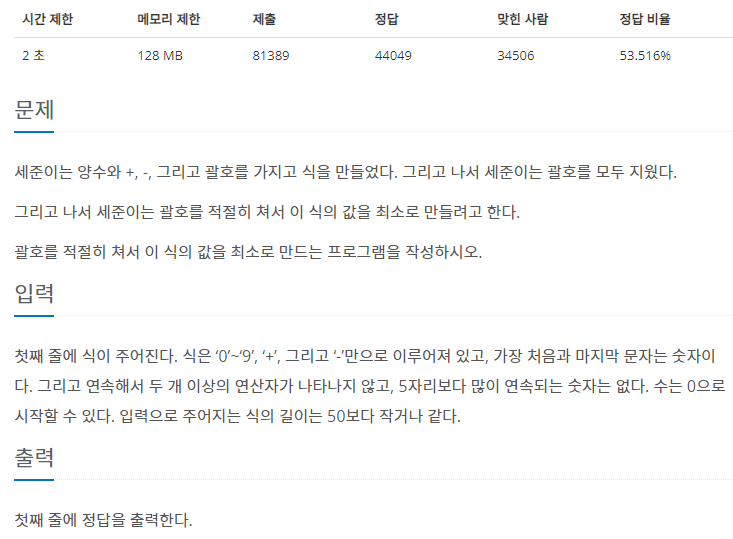
문제

접근 방식

주어진 식에 적절히 괄호를 추가해 가장 작은 결과를 얻어야 하는데

간단하게 생각해 보면 - 부호가 등장한 이후에 나오는 모든 숫자들을

- 부호가 재등장하기 전까지 빼주면 된다.

55-50+40-50+40+30-50

예를 들어 위와 같은 식이 주어졌다면

55-(50+40)-(50+40+30)-(50)

이렇게 괄호를 추가해 계산하는 것이 가장 작은 결과를 얻는다.

55-((50+40)-(50+40+30)-(50))

조금만 더 생각해 보면 첫 - 부호 등장 이후에 오는 모든 수들은

복잡하게 생각할 필요 없이 빼도 상관이 없다는 것을 알 수 있다.

그래서 처음으로 -부호가 등장하기 전까지만 값을 더해주고

이후에 오는 모든 수들은 빼주면 된다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		String input = br.readLine();

		int sum = 0;
		int len = 0;
		int num;
		char c;
		boolean isMinus = false;

		for (int i = 0; i < input.length(); i++) {
			c = input.charAt(i);

			if (Character.isDigit(c)) len++;

			if (c == '-') {
				isMinus = true;
				continue;
			}

			if (i == input.length() - 1 || !Character.isDigit(input.charAt(i + 1))) {
				num = Integer.parseInt(input.substring(i + 1 - len, i + 1));
				len = 0;

				if (isMinus) sum -= num;
				else sum += num;
			}
		}

		System.out.println(sum);
	}
}

문제

접근 방식

싼 값에 주식을 사고 비싼 값에 팔면 가장 이득을 볼 수 있다는 당연한 사실을 통해

주어진 주가를 역으로 탐색해 현재 가장 큰 값보다 비싼 값을 만날 때까지

이전의 모든 주식을 산 후에 팔아주면 된다.

3 2 4 5 7 8 6 9 8 4 5

예를 들어 위와 같이 주가 목록이 주어졌을 때 역으로 탐색하면

5를 기준으로 더 큰 값인 8을 만나기 전까지 주식을 사면

4원에 주식을 산 후에 5원에 팔아서 1원 이득을 볼 수 있고

다시 8을 기준으로 더 큰 값이 9를 만나기 전까지는

어떠한 주식도 살 수 없기 때문에 8을 그대로 팔아 0원 이득을 볼 수 있으며

다시 9를 기준으로 더 큰 값이 없으므로 남은 모든 주식을 사면

(9원 * 7일) - (3 + 2 + 4 + 5 + 7 + 8 + 6) = 63 - 35 = 28

28원 만큼의 이득을 볼 수 있다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		StringBuilder sb = new StringBuilder();

		int t = Integer.parseInt(br.readLine());
		int n;
		int[] arr;

		while (t-- > 0) {
			n = Integer.parseInt(br.readLine());
			st = new StringTokenizer(br.readLine());
			arr = new int[n];

			for (int i = 0; i < n; i++) {
				arr[i] = Integer.parseInt(st.nextToken());
			}

			long profit = 0;
			long max = 0;
			long sum = 0;
			long count = 0;

			for (int i = n - 1; i >= 0; i--) {
				long price = arr[i];

				if (max == 0) {
					max = price;
					continue;
				}

				if (i == 0) {
					if (price <= max) {
						count++;
						sum += price;
					}
					profit += (count * max - sum);
					continue;
				}

				if (max >= price) {
					count++;
					sum += price;
				} else {
					profit += (count * max - sum);
					count = 0;
					sum = 0;
					max = price;
				}
			}

			sb.append(profit).append("\n");
		}

		System.out.println(sb);
	}
}

문제

접근 방식

10, 30, 20, 50, 40, 80, 70, 60

만약 위와 같은 로프들이 주어졌을 때를 생각해보면

8개의 로프를 모두 사용한 경우에는 가장 낮은 무게를 들 수 있는

10kg짜리 로프에 맞춰야하기 때문에 80kg를 들 수 있지만

7개를 사용하는 경우에는 20kg에 맞춰서 140kg을 들 수 있다.

10, 20, 30, 40, 50, 60, 70, 80

80, 140, 180, 200, 200, 180, 140, 80

정렬을 해서 n개의 추를 사용하는 경우를 모두 계산해보면 위와 같다.

결국 정렬을 한 후에 n개를 골랐을 때마다 가능한 무게를 계산하고

그 중에서 가장 큰 값이 정답이 된다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		int n = Integer.parseInt(br.readLine());

		int[] weights = new int[n];

		for (int i = 0; i < n; i++) weights[i] = Integer.parseInt(br.readLine());

		Arrays.sort(weights);

		int max = 0;

		for (int i = 0; i < n; i++) max = Math.max(max, weights[i] * (n - i));

		System.out.println(max);
	}
}

문제

접근 방식

DP를 이용해서 O(N^2) 풀이를 생각할 수도 있지만 주어진 입력과 제한 시간으로는

해당 시간 복잡도로는 풀 수 없는 문제다.

간단하게 생각해 보면 가장 많은 회의를 배정하기 위해서는

가장 빨리 끝나는 회의들만 골라주면 된다.

1 4
3 5
0 6
5 7
3 8
5 9
6 10
8 11
8 12
2 13
12 14

위의 경우를 예로 들면 첫 번째 회의가 가장 빠른 4시에 끝나니

이 회의를 고른 후에 다음으로 4시 이후에 시작하는 다른 회의를 골라야

가장 효율적으로 회의를 배정할 수 있는 것을 알 수 있다.

1, 4 
3, 5
0, 6
5, 7
3, 8
5, 9
6, 10
8, 11 
8, 12 
2, 13 
12, 14

위는 주어진 회의 시간들을 끝나는 시간이 가장 빠른 순으로 정렬하고

끝나는 시간이 같은 경우에는 시작하는 시간이 빠른 순으로 정렬해 준 결과다.

정렬한 뒤에 보면 {1, 4}, {5, 7}, {8, 11}, {12, 14}를 선택하는 것이

가장 효율적이라는 것을 더 알기 쉽게 볼 수 있다.

즉, 정렬을 수행한 후에 시작 시간이 현재까지 기록된

가장 빠른 끝나는 시간보다 크거나 같은 경우가

다음에 올 수 있는 가장 최적의 회의 배정이므로

반복문을 한 번만 수행하여 회의실을 배정할 수 있다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;

		int n = Integer.parseInt(br.readLine());
		int[][] times = new int[n][2];

		for (int i = 0; i < n; i++) {
			st = new StringTokenizer(br.readLine());

			times[i][0] = Integer.parseInt(st.nextToken());
			times[i][1] = Integer.parseInt(st.nextToken());
		}

		Arrays.sort(times, (o1, o2) -> o1[1] != o2[1] ? o1[1] - o2[1] : o1[0] - o2[0]);

		int min = -1;
		int count = 0;

		for (int i = 0; i < n; i++) {
			if (min <= times[i][0]) {
				count++;
				min = times[i][1];
			}
		}

		System.out.println(count);
	}
}

문제

접근 방식

문제 자체는 간단한데 어떻게 풀어야 할지 어려웠던 문제였지만

일단 규칙을 찾아야 할 거 같아서 수들을 적다 보니 특징을 발견해서 풀 수 있었다.

1	10	101
2	12	121 123
3	21	210 212
4	23	232 234
5	32	
6	34
7	43
8	45
9	54	(생략)
	56
	65
	67
	76
	78	787 789
	87	876 878
	89	898
	98	987 989

각각 한 자리부터 세 자리까지의 쉬운 계단 수를 나열한 목록인데

0과 9로 끝나는 부분만 제외한 모든 수들이 2배씩 늘어나고

0과 9로 끝나는 경우만 그대로 하나인 것을 알 수 있다.

0으로 끝나는 경우에는 09가 될 수 없으니 01만 올 수 있고

9로 끝나는 경우도 마찬가지로 90이 될 수 없으니 98만 올 수 있다.

0과 9를 제외한 1~8로 끝나는 수들은 전부 자기 자신 - 1, 자기 자신 + 1

이렇게 두 가지로 늘어날 수 있기 때문에 이 특징들을 이용해 계산해 주면 된다.

우선 DP 테이블은 각 자릿수별로 특정 숫자로 끝나는 가짓수를 기록하기 위해

다음과 같이 2차원 배열로 정의했다.

dp[n][10] = 1 ~ n번째 자리수의 0 ~ 9로 끝나는 경우의 수

이제 위에서 정리한 쉬운 계단 수의 특징들을 가지고 테이블을 채워주면 되는데

0과 9의 경우는 기존 가짓수를 그대로 따라가기 때문에

d[i][0] = d[i-1][1]
d[i][9] = d[i-1][8]

위와 같이 이전 값을 그대로 기록해주면 된다.

각각 이전 자리수의 0번과 9번 값을 가져오지 않고 1번과 8번을 가져오는 이유는

이전 자리수가 1인 경우에만 10처럼 0으로 끝날 수 있고

이전 자리수가 8인 경우에만 89처럼 9로 끝날 수 있기 때문이다.

d[i][j] = d[i-1][j-1] + d[i-1][j+1]

2 ~ 8의 경우에는 이전 자릿수의 j-1과 j+1인 경우에 j가 될 수 있으니

두 값을 모두 더해주면 된다.

풀이

public class Main {

	private static final int MOD = 1_000_000_000;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		byte n = Byte.parseByte(br.readLine());

		long[][] dp = new long[n + 1][10];

		dp[1] = new long[]{0, 1, 1, 1, 1, 1, 1, 1, 1, 1};

		for (byte i = 2; i <= n; i++) {
			dp[i][0] = dp[i - 1][1] % MOD;
			dp[i][9] = dp[i - 1][8] % MOD;
			for (byte j = 1; j < 9; j++) {
				dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j + 1]) % MOD;
			}
		}

		long count = 0;

		for (byte i = 0; i < 10; i++) {
			count += dp[n][i];
		}

		System.out.println(count % MOD);
	}
}

문제

접근 방식

문제 자체는 14501번 퇴사 문제와 똑같지만 입력의 양이 최대 150만 개이기 때문에

이전에 풀었던 방식처럼 O(n^2)의 시간 복잡도로 풀면 시간 초과가 발생한다.

DP 테이블을 좀 더 효율적으로 채워 넣어야 시간 제한을 맞출 수 있으니

문제를 좀 더 자세하게 분석해보겠다.

우선 i번째 날에 t일의 시간이 소요되는 상담을 진행했다면

i + 1일에 p만큼의 돈을 지급받는다.

즉, i일 이전에 받은 돈들은 모두 정해진 기한 내에 완료하여 받을 수 있는 돈이고

i일에 받을 수 있는 가장 큰돈은 i일 이전의 값들 중 가장 큰 값이다.

n
10

t p
5 50
4 40
3 30
2 20
1 10
1 10
2 20
3 30
4 40
5 50

위와 같은 테스트 케이스가 주어졌을 때

1 ~ 5일까지의 상담들은 모두 6일에 완료되어 돈을 받을 수 있고

그중 가장 큰 값인 50원이 6일에 받을 수 있는 가장 큰 경우다.

다음으로 6일에 진행한 상담비는 하루 뒤인 7일에 받을 수 있고

7일에는 이전까지의 받은 돈 중 가장 큰 값인 50원에

당일 받을 10원을 더한 60원을 받을 수 있다.

7일에 진행한 상담비는 2일 뒤인 9일에 받을 수 있고

마찬가지로 현재까지 받은 돈 중 가장 큰 60원에

당일 받을 20원을 더한 80원을 받을 수 있다.

8일에 진행한 상담비는 3일 뒤인 퇴사날에 받을 수 있고

8일 이전의 가장 큰 값인 60원에 30원을 더한 90원을 받을 수 있다.

즉, 매 상담마다 두 가지를 계산해 주면 되는데

현재를 기준으로 가장 큰돈을 받을 수 있는 경우인 dp [i]와

현재 + 소요일에 받게 될 돈인 dp [i+t]를 구해주면 된다.

dp[i]는 현재 날짜와 이전 날짜 중에서 가장 큰 값을 골라주면 되니

dp[i] = max(dp[i], dp[i-1])

dp [i+t]는 현재 날짜에 받을 수 있는 가장 큰 돈 + 상담 완료 시 받을 돈 중에서

가장 큰 값을 골라줘야 하니

dp[i+t] = max(dp[i+t], dp[i] + p)

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;

		int n = Integer.parseInt(br.readLine());

		int[] dp = new int[n + 51];

		for (int i = 1; i <= n; i++) {
			st = new StringTokenizer(br.readLine());

			int time = Integer.parseInt(st.nextToken());
			int price = Integer.parseInt(st.nextToken());

			dp[i] = Math.max(dp[i], dp[i - 1]);
			dp[i + time] = Math.max(dp[i + time], dp[i] + price);
		}

		System.out.println(Math.max(dp[n], dp[n + 1]));
	}
}

문제

접근 방식

문제에 나와 있는 예시를 살펴보면

4일의 경우에는 1일과 3일 중 하나를 선택할 수 있고

둘 중 더 큰 값을 선택하는 것이 효율적이니

더 큰 값을 골라주면 된다. (예시에서 두 날의 값은 같아서 뭘 고르든 상관은 없다.)

즉, 현재 날을 기준으로 이전에 상담이 끝나는 요일들 중

가장 비용이 큰 값을 선택해주면 된다.

DP 테이블은 아래와 같이 정의했다.

dp[i] = i번째 날에 받을 수 있는 누적 금액

dp[i] = 1 ~ i-1까지의 날짜 중 i일 이전에 끝나고 가장 비용이 큰 값

위의 과정을 코드로 작성하면 된다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;

		int n = Integer.parseInt(br.readLine());

		int[] times = new int[n + 1];
		int[] prices = new int[n + 1];

		for (int i = 1; i <= n; i++) {
			st = new StringTokenizer(br.readLine());

			times[i] = Integer.parseInt(st.nextToken());
			prices[i] = Integer.parseInt(st.nextToken());
		}

		int[] d = new int[n + 1];
		int result = 0;

		for (int i = 1; i <= n; i++) {
			if (i + times[i] - 1 > n) continue;

			int max = prices[i];

			for (int j = 1; j < i; j++) {
				if (j + times[j] - 1 < i) max = Math.max(prices[i] + d[j], max);
			}

			d[i] = max;
			result = Math.max(max, result);
		}

		System.out.println(result);
	}
}

문제

접근 방식

각 변의 길이가 1인 정삼각형으로 시작해 n번째 정삼각형의 한 변의 길이를 구해야 한다.

삼각형을 위와 같이 나선 모양으로 회전하면서 추가할 때

위와 같이 한 변의 길이가 이전 변의 길이보다 커질 때 새로운 삼각형을 추가해주고

이 때 새로운 정삼각형의 새로운 한 변의 길이는 dp[i] = dp[i - 1] + dp[i - 5]라는 것을 알 수 있다.

dp[i-5]를 계산하기 위해 dp 테이블의 dp[1] ~ dp[5]까지를

각각 순서대로 1, 1, 1, 2, 2로 초기화 해준 후에

dp[6] ~ dp[n]까지 구한 공식대로 계산해주면 된다.

계산하다 보면 인트형의 범위를 벗어나니 long 타입으로 저장해줘야 한다.

풀이

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();

		int t = Integer.parseInt(br.readLine());

		long[] dp = new long[101];

		dp[1] = 1;
		dp[2] = 1;
		dp[3] = 1;
		dp[4] = 2;
		dp[5] = 2;


		for (int i = 6; i <= 100; i++) {
			dp[i] = dp[i - 1] + dp[i - 5];
		}

		while (t-- > 0) {
			int n = Integer.parseInt(br.readLine());

			sb.append(dp[n]).append("\n");
		}

		System.out.println(sb);
	}
}