문제

접근 방식
배열에서 특정 부분만 확인 했을 때 팰린드롬인지 판별하는 문제다.
DP 문제이긴 하지만 이전 값을 사용해 테이블을 채워나가는 방식은 아니고
길이별로 팰린드롬인지 직접 확인해서 테이블에 저장해
s와 e를 입력 받을 때마다 매번 계산하지 않고 저장된 값을 읽는 방식이다.
1, 2, 1, 3, 1, 2, 1
위와 같은 배열의 경우에는 다음과 같은 테이블이 만들어진다.
| 1 | 2 | 1 | 3 | 1 | 2 | 1 | |
| 1 | T | F | T | F | F | F | T |
| 2 | T | F | F | F | T | F | |
| 1 | T | F | T | F | F | ||
| 3 | T | F | F | F | |||
| 1 | T | F | T | ||||
| 2 | T | F | |||||
| 1 | T |
숫자가 하나인 경우는 무조건 팰린드롬이니 참으로 설정해두고
2개 이상인 경우만 판단하면 되고, 시작점이 끝점보다 큰 경우는 없기 때문에
자기 자신의 인덱스 이전은 신경 쓸 필요가 없다.
1 ~ 2번이 팰린드롬인지, 1 ~ 3번이 팰린드롬인지, ..., 1 ~ 7번이 팰린드롬인지
2 ~ 3번이 팰린드롬인지, 2 ~ 4번이 팰린드롬인지, ..., 2 ~ 7번이 팰린드롬인지
...
...
5 ~ 6번이 팰린드롬인지, 5 ~ 7번이 팰린드롬인지
6 ~ 7번이 팰린드롬인지
이중 반복문을 돌면서 위와 같이 다 검증해주면서 테이블만 채워주면 된다.
풀이
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int n = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int[] seq = new int[n + 1];
boolean[][] dp = new boolean[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
seq[i] = Integer.parseInt(st.nextToken());
dp[i][i] = true;
}
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
if (isPalindrome(seq, i, j)) dp[i][j] = true;
}
}
int m = Integer.parseInt(br.readLine());
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
sb.append(dp[Integer.parseInt(st.nextToken())][Integer.parseInt(st.nextToken())] ? 1 : 0).append("\n");
}
System.out.println(sb);
}
private static boolean isPalindrome(int[] seq, int s, int e) {
while (s < e) {
if (seq[s++] != seq[e--]) return false;
}
return true;
}
}
'Java > Algorithms' 카테고리의 다른 글
| [백준] 11660번 : 구간 합 구하기 5 (1) | 2024.03.22 |
|---|---|
| [백준] 2011번 : 암호코드 (0) | 2024.03.19 |
| [백준] 1915번 : 가장 큰 정사각형 (1) | 2024.03.17 |
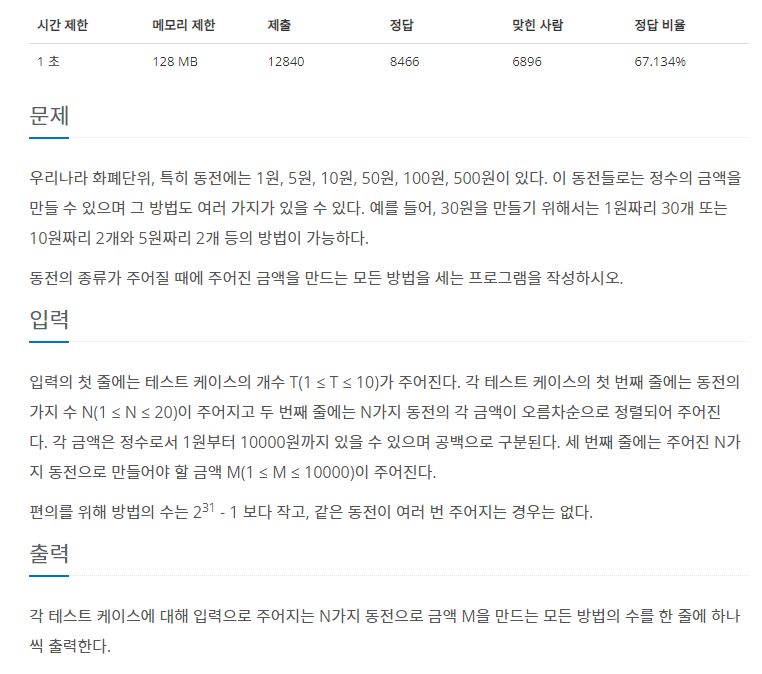
| [백준] 2294번 : 동전2 (0) | 2024.03.16 |
| [백준] 9084번 : 동전 (0) | 2024.03.16 |