728x90
문제

접근 방식
분리 집합과 유니온 파인드에 대해서 아직 배우지 않아
기존에 풀었던 4803번 문제와 비슷하게 풀면 풀 수 있겠다 생각이 들어
무작정 시도해봤는데 어찌저찌 풀었다.
우선 이번 문제는 그래프가 주어졌을 때
간선을 지우거나 추가하여 하나의 트리로 만들기 위한
총 횟수를 구해야 한다.
간단하게 생각하면
한 정점에서 방문할 수 있는 모든 정점을 방문했을 때
사이클이 존재하지 않는다면 이미 하나의 트리니
기존의 트리와 합치기만 하면 될 것이고
그렇지 않다면 간선을 제거해주고 합쳐주면 된다.
사이클이 존재하는 경우에 몇 개의 간선을 제거해야 하는지는
트리의 규칙을 생각해보면 쉬운데
정점 N개의 트리는 N-1개의 간선을 가지고 있으니
현재까지 발견한 간선의 수 - (N - 1) = 삭제해야 할 간선의 수
라는 것을 알 수 있다.
발그림으로나마 더 쉽게 설명하자면
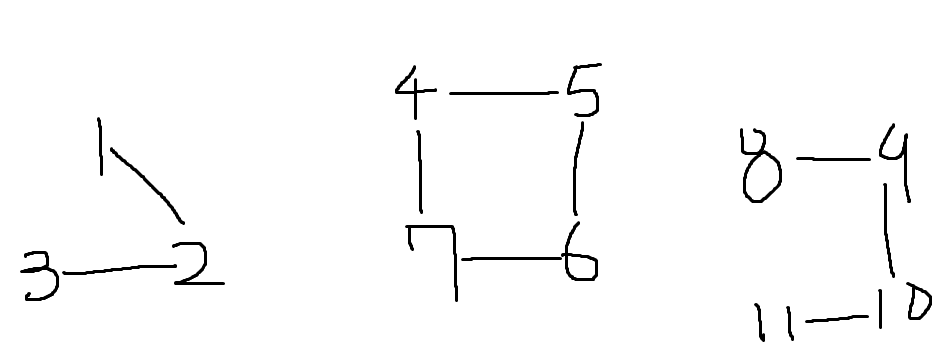
위와 같이 그래프가 주어졌을 때,
1-2-3은 이미 트리니 그대로 두고
4-5-6-7은 간선의 개수가 N-1보다 하나 더 많으니
간선을 하나 잘라주고
8-9-10-11도 이미 트리니 그대로 두면 된다.
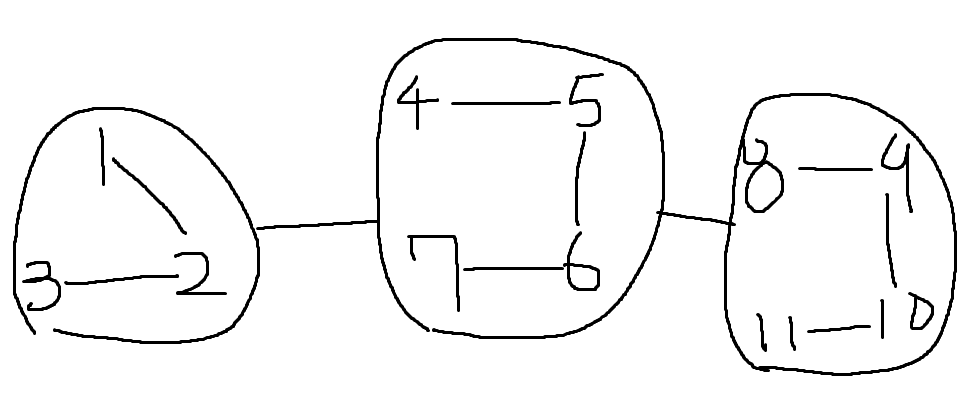
이제 세 트리를 위와 같이 서로 이어주면 되는데
이 경우도 마찬가지로, 각각의 트리를 정점이라 생각했을 때
N-1개 만큼 간선을 추가해주면 된다.
풀이
public class Main {
private static int node, edge;
private static boolean[] isVisited;
private static final ArrayList<ArrayList<Integer>> near = new ArrayList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int x, y;
int cut = 0;
int tree = 0;
isVisited = new boolean[n + 1];
for (int i = 0; i <= n; i++) {
near.add(new ArrayList<>());
}
while (m-- > 0) {
st = new StringTokenizer(br.readLine());
x = Integer.parseInt(st.nextToken());
y = Integer.parseInt(st.nextToken());
near.get(x).add(y);
near.get(y).add(x);
}
for (int i = 1; i <= n; i++) {
if (isVisited[i]) continue;
tree++;
node = edge = 0;
dfs(i);
if (edge != (node - 1) * 2) {
cut += (edge - ((node - 1) * 2))/2;
}
}
System.out.println(cut + tree - 1);
}
private static void dfs(int cur) {
isVisited[cur] = true;
node++;
for (int next : near.get(cur)) {
edge++;
if (isVisited[next]) continue;
dfs(next);
}
}
}
'Java > Algorithms' 카테고리의 다른 글
| [백준] 2250번 : 트리의 높이와 너비 (0) | 2024.01.29 |
|---|---|
| [백준] 14267번 : 회사 문화 1 (1) | 2024.01.29 |
| [백준] 1240번 : 노드사이의 거리 (0) | 2024.01.28 |
| [백준] 15681번 : 트리와 쿼리 (0) | 2024.01.28 |
| [백준] 4803번 : 트리 (1) | 2024.01.28 |